Building a Movie Review Sentiment Classifier: Naive Bayes on the IMDB Dataset with Streamlit Demo
6/27/20252 min read


Introduction to Sentiment Analysis
Movie reviews are a goldmine of perspectives. Some love a film, others can’t stand it.
Automatically classifying whether a review is positive or negative can help studios streaming services, and marketers understand audiences better.
In this blog, we’ll build a sentiment classifier using Naive Bayes on the popular IMDB dataset and wrap it up with a Streamlit web app so you can test reviews live!
Understanding the IMDB Dataset
The IMDB dataset has 50 thousand movie reviews for natural language preprocessing or text analysis tasks. This data set will be great for Binary Classification.
We will use the data set split into two sets - training and testing. Each will contain 25k reviews. The classes are either positive or negative.
We will train our machine learning model with 25K labelled reviews and then see how our model works with the other half.
Here is the link to the data set in my Github repo.
If you are a Kaggle lover - can check or download the data-set from Kaggle.
Implementing the Naive Bayes Classifier
Naive Bayes is based on a probability theorem called the Bayes' Theorem. It predicts the class by measuring the conditional probabilities.
The probability based classification algorithm works with independent features.
This means that each feature is considered to be contributing independently to the probability of the predicted class.
That is the "Naive" part - which is basically making calculations simple and efficient. Now lets see what is the Bayes' Theorem which is the heart of Naive Bayes Classifier.
Bayes' Theorem
This theorem is actually named after Reverend Thomas Bayes (1701–1761).
Let us take two events A and event B.
The conditional probability of event A provided that event B happens is equal to the probability of B provided event A multiplied with the probability of A up on the probability of event B. That is P(A|B) = P(B|A) * P(A) /P(B)
If we consider statistical terms then P(B|A) can be said the likelihood of B given A.
And P(A) is basically the prior probability of event A.
And probability P(B) = marginal probability of event B.
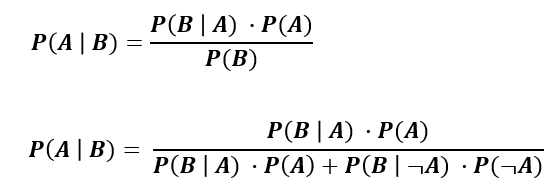
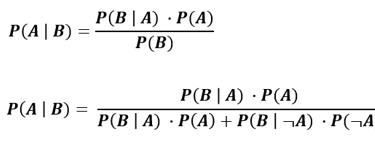
You can experiment with different probability values in the below calculator. The calculator works on the Bayes' Theorem.
Setting up the Environment
Firstly when ever you are working with some machine learning or data science project you must first create a virtual environment.
Create a python virtual environment. Here I have put up all the related steps for your reference:
Installing required Libraries
For this experiment we will require libraries like: wordcloud, pandas, matplotlib, plotly, scikit-learn, numpy, nltk.
